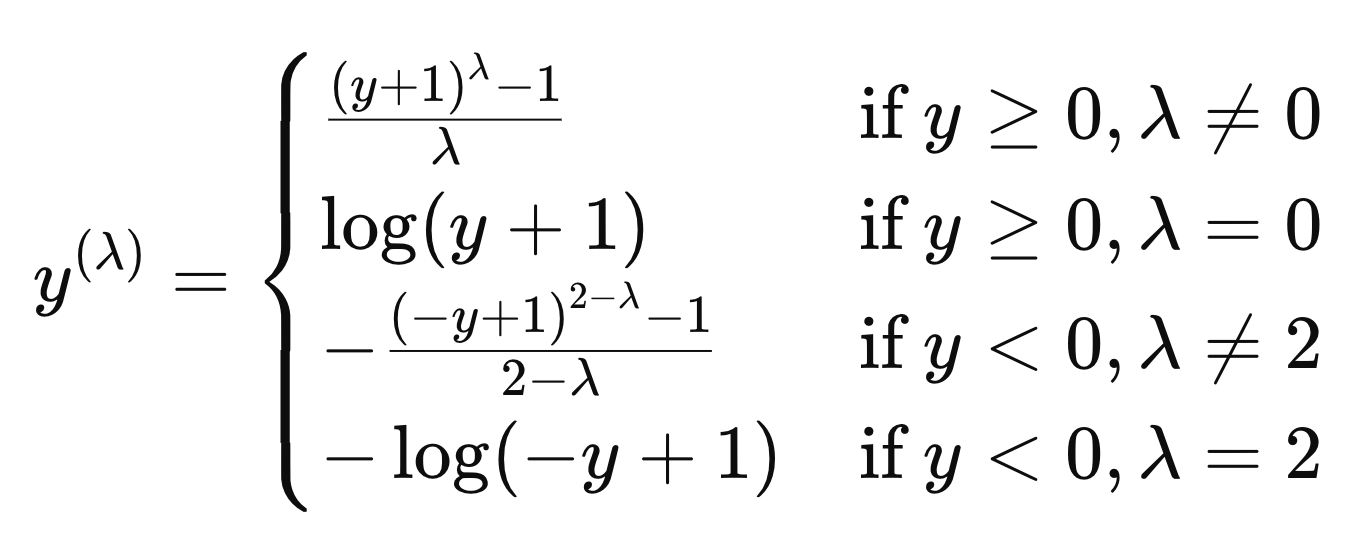Handle Numerical Variable Transformation

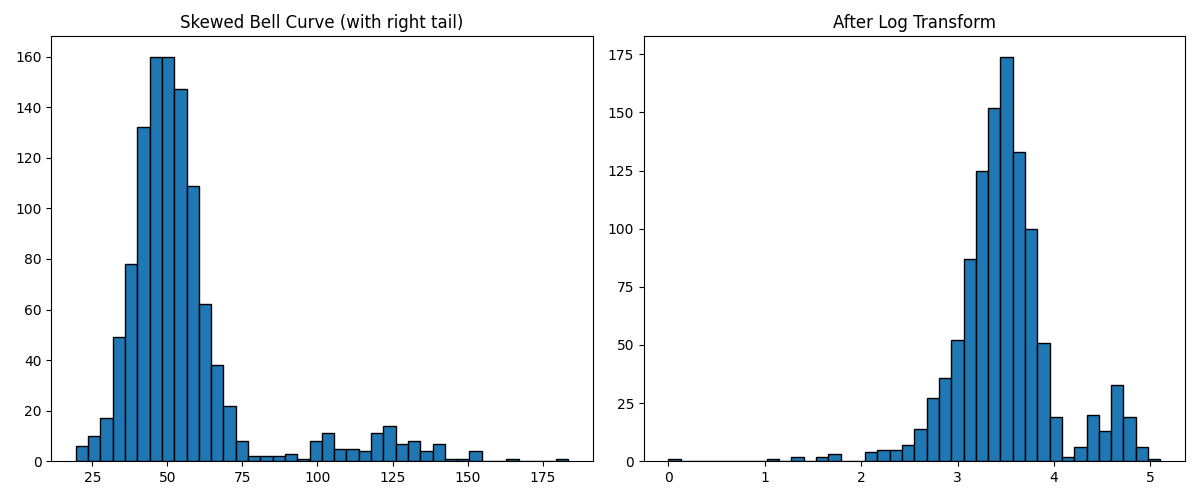
Log Transformer

It applies the natural logarithm (base e) or the base 10 logarithm to numerical variables.

Reduce skewness (normalise distributions) - Many real-world variables are positively skewed (long tail to the right), like income, sales, or house prices. Applying log compresses large values and stretches small ones, making the distribution more symmetric.

Parameters:

• base : 'e' for natural or '10' for base 10. Natural is default if the parameter is missing.
• variables: Specify which columns to apply the transformer to, if missing it will apply to all numerical fields.

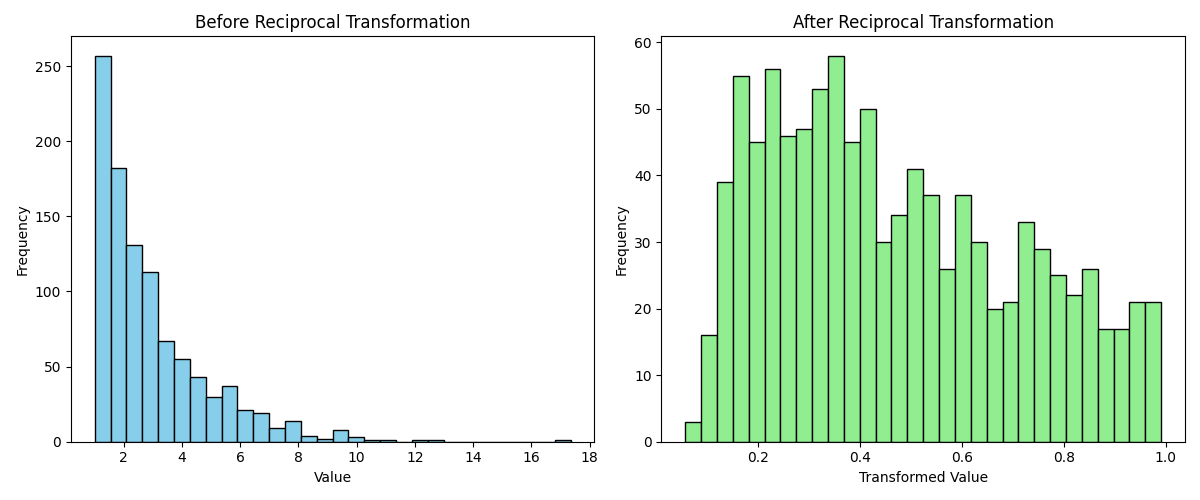
Reciprocal Transformer

This technique applies the reciprocal transformation 1 / x to numerical variables.

Consider use when your data is right-skewed (most values are small, with a few very large values), the reciprocal transformation can pull in large values and stretch out small values, making the distribution more symmetric. It is useful when we have ratios, that is, values resulting from the division of two variables.

Power Transformer

It applies power or exponential transformations to the numerical variable. As general guidance, if data is right-skewed (i.e. more observations around lower values), use exp <1. If data is left-skewed (i.e. more observations around higher values), use exp >1.

Parameters:

• exp : the power (or exponent), default is 0.5.

Box Cox Transformer

This transformer applies the following mathematical formula, note: the data must be positive for this transformer:

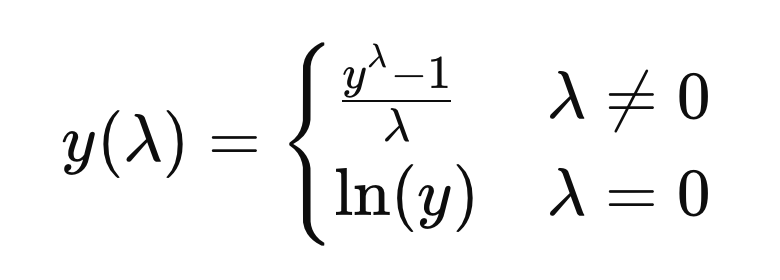
The Box Cox transformation is used to reduce or eliminate variable skewness and obtain features that better approximate a normal distribution.

Yeo Johnson Transformer

The Yeo-Johnson transformation is an extension of the Box-Cox transformation that is no longer constrained to positive values. In other words, the Yeo-Johnson transformation can be used on variables with zero and negative values as well as positive values. Its formula is: