Measure of Central Tendency

Measures of Central Tendency are statistical values that identify the centre or typical value of a dataset.
They describe where most data points tend to cluster and give a single value that best represents the entire dataset.

Why It Matters

• Helps summarise large datasets with one representative number.
• Provides a quick overview of data distribution.
• Used to compare datasets and identify trends.
• In machine learning, it’s often used in data exploration, normalisation, and feature understanding.

The Three Main Measures

1. Mean (Arithmetic Average)

• Definition: The sum of all data values divided by the number of observations.
• Formula:

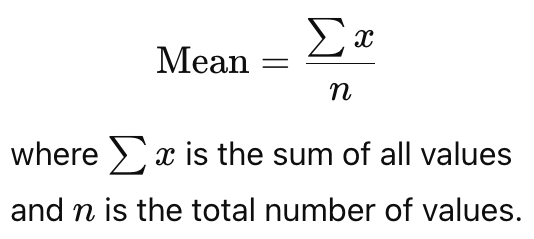
• Example:
• • Data: [4, 6, 8] so the mean = (4 + 6 + 8) ÷ 3 = 6
• Notes:
• • Sensitive to extreme values (outliers).
  • Used for interval and ratio data.

2. Median (Middle Value)

• Definition: The middle value when all data points are arranged in order (ascending or descending).
• • If the dataset has an even number of values, the median is the average of the two middle values.
• Example:
• • Data: [3, 5, 7, 9, 11] → Median = 7
  • Data: [3, 5, 7, 9] → Median = (5 + 7) ÷ 2 = 6
• Notes:
• • Unaffected by outliers, making it useful for skewed data.
  • Suitable for ordinal, interval, and ratio data.

3. Mode (Most Frequent Value)

• Definition: The value that appears most frequently in a dataset.
• A dataset can have:
• • One mode (unimodal),
  • More than one mode (bimodal or multimodal), or
  • No mode (if all values occur equally).
• Example:
• • Data: [2, 4, 4, 6, 8] → Mode = 4
• Notes:
• • Works for nominal, ordinal, interval, and ratio data.
  • Useful for categorical variables (e.g., most common product purchased).

Summary

In Machine Learning

• Used during exploratory data analysis (EDA) to understand feature distributions.
• The mean may be used for imputation of missing values.
• The median is preferred when data are skewed (e.g., income, house prices).
• The mode helps understand dominant categories in categorical data.

Calculating Mean, Median and Mode in Python

Using the statistics module (built-in):

Mode only works if there is a single mode value.

Using NumPy (for numerical arrays and larger datasets)

Mode returns an array of all modes.

Using Pandas (for data series)

Mode returns a data series of all modes.