Probability

Probability is the measure of how likely an event is to occur.
It ranges from 0 (impossible) to 1 (certain).

In machine learning and data science, probability helps:

• Model uncertainty (e.g., how likely a prediction is correct)
• Build probabilistic models (e.g., Naive Bayes, Bayesian networks)
• Support decision-making under uncertainty
• Enable sampling, randomisation, and evaluation of model reliability

Basic Formula

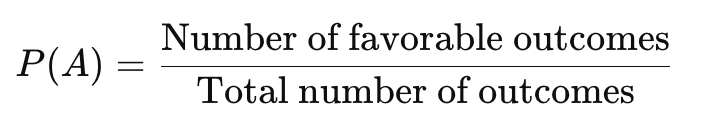
Example:
If a dataset has 100 samples and 20 belong to class A,
then P(A) = 20/100 = 0.2

Addition Rules of Probability

Used when we want the probability of either one event or another happening.
That is, P(A or B).

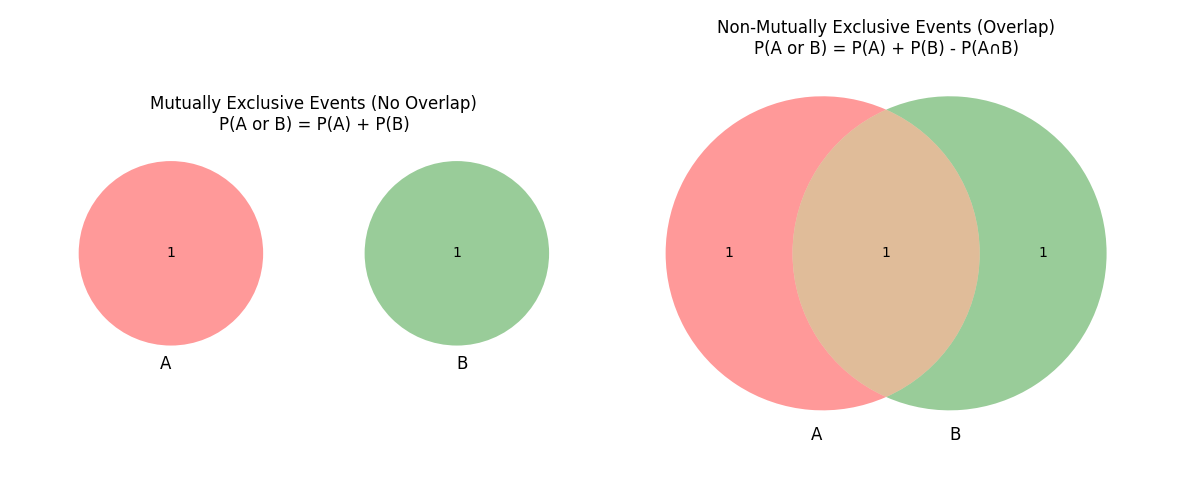
1. Addition Rule for Mutually Exclusive Events

Two events are mutually exclusive if they cannot occur at the same time.
(i.e., the occurrence of one event means the other cannot happen.)

Formula:

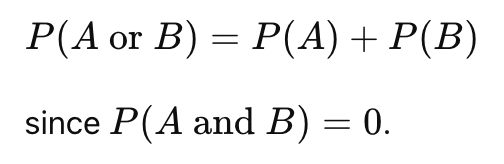
Example:

Rolling a die:

• Event A = rolling a 2 → P(A) = 1/6
• Event B = rolling a 4 → P(B) = 1/6
• These are mutually exclusive (you can’t roll both).
• So:
• P(A or B) = 1/6 + 1/6 = 2/6 = 1/3

2. Addition Rule for Non-Mutually Exclusive Events

Two events are not mutually exclusive if they can occur together (overlap).

Formula:

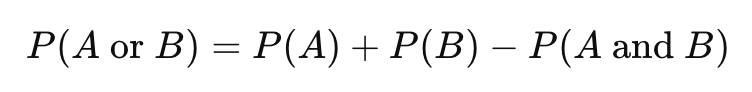
We subtract the overlap so it isn’t counted twice.

Example:

In a dataset:

• Event A = person likes apples (40%)
• Event B = person likes oranges (30%)
• Both (A and B) = 10%
• Then:
• P(A or B) = 0.4 + 0.3 − 0.1 = 0.6

So, 60% of people like either apples or oranges (or both).

Multiplication Rules of Probability

Used when we want the probability that two events occur together —
that is, P(A and B).

1. Multiplication Rule for Independent Events

Two events are independent if the outcome of one does not affect the other.

Formula:

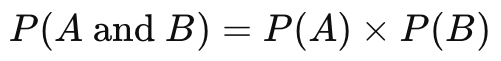
Example:

Flipping a coin (event A) and rolling a die (event B):

• P(A=Heads) = 1/2
• P(B=6) = 1/6
• Since they’re independent:
• P(A and B) = (1/2) × (1/6) = 1/12

2. Multiplication Rule for Dependent Events

Two events are dependent if one influences the probability of the other.

Formula:

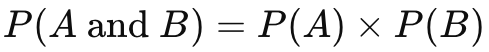
where P(B ∣ A) means “the probability of B given A has occurred.”

Example:

Suppose 30% of emails are spam.

• Of those spam emails, 80% contain links.
• P(Spam) = 0.3, P(Link ∣ Spam) = 0.8
• So:
• P(Spam and Link) = 0.3 × 0.8 = 0.24

Interpretation:
There’s a 24% chance that an email is both spam and contains a link.