Uniform Distribution

The Uniform Distribution is a probability distribution in which all outcomes are equally likely.

That means:

Every value within a given range has the same probability of occurring.

There are two main types:

• Discrete Uniform Distribution → finite number of equally likely outcomes (e.g., rolling a fair die)
• Continuous Uniform Distribution → infinite number of equally likely values within an interval [a,b]

1. Continuous Uniform Distribution

Probability Density Function (PDF)

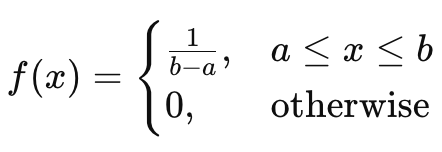
Where:

• a = minimum value
• b = maximum value
• f(x) = constant height (flat line)

The total area under the curve = 1.

Cumulative Distribution Function (CDF)

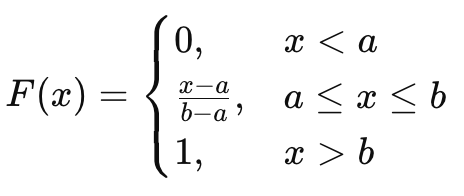
The CDF increases linearly from 0 → 1 as x moves from a to b.

Examples

• Random number between 0 and 1 - Every number equally likely
• Bus arrival time (if unknown within hour) - Any minute equally likely
• Random pixel intensity - Equal chance for any grayscale value

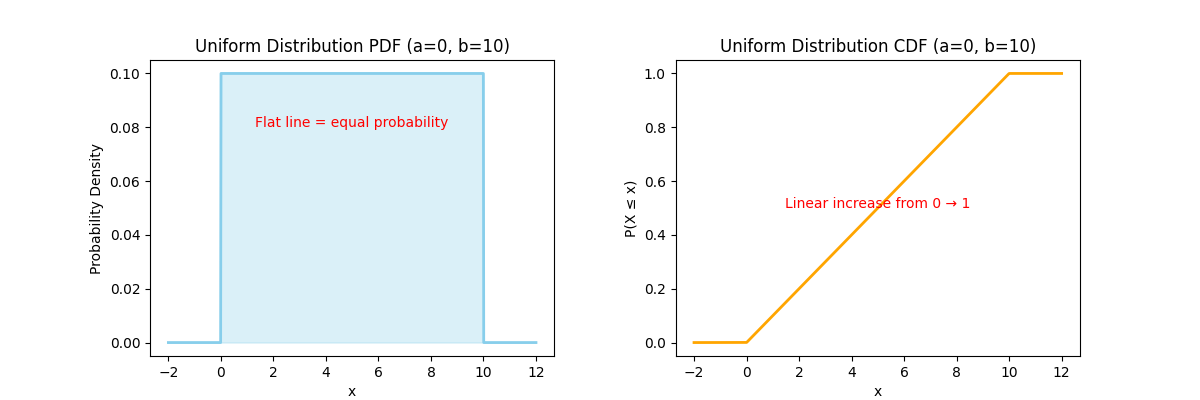
• Left Plot (PDF) → a flat, horizontal line between a=0 and b=10, showing all values are equally likely.
• Right Plot (CDF) → a straight, diagonal line increasing from 0 to 1, showing cumulative probability grows evenly.

The total area under the PDF = 1
The slope of the CDF = constant (since probability is uniform)

2. Discrete Uniform Distribution

A Discrete Uniform Distribution has a finite set of equally likely outcomes.

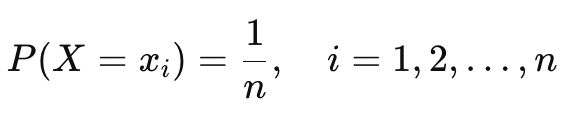
Where nnn = number of possible outcomes.

Example

Rolling a fair 6-sided die:

Every outcome is equally likely, just like in the continuous case but with discrete values.

In Machine Learning

• Random initialisation - Weights or biases initialised from a uniform range
• Random sampling - Generating random feature subsets or values
• Monte Carlo simulations - Random uniform sampling for probability estimation
• Data augmentation - Random transformations drawn from uniform ranges
• Synthetic data generation - Evenly distributed continuous random values